Ekman layer
The Ekman layer is the layer in a fluid where there is a force balance between pressure gradient force, Coriolis force and turbulent drag. It was first described by Vagn Walfrid Ekman.
Contents |
History
Ekman developed the theory of the Ekman layer after Fridtjof Nansen observed that ice drifts at an angle of 20°-40° to the right of the prevailing wind direction while on an Arctic expedition aboard the Fram. Nansen asked his colleague, Vilhelm Bjerknes to set one of his students upon study of the problem. Bjerknes tapped Ekman, who presented his results in 1902 as his doctoral thesis.[1]
Mathematical formulation
The mathematical formulation of the Ekman layer can be found by assuming a neutrally stratified fluid, with horizontal momentum in balance between the forces of pressure gradient, Coriolis and turbulent drag.
where 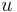 and
and 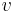 are the velocities in the
are the velocities in the 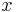 and
and 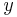 directions, respectively,
directions, respectively, 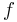 is the local Coriolis parameter, and
is the local Coriolis parameter, and 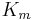 is the diffusive eddy viscosity, which can be derived using mixing length theory.
is the diffusive eddy viscosity, which can be derived using mixing length theory.
Boundary conditions
There are many regions where an Ekman layer is theoretically plausible; they include the bottom of the atmosphere, near the surface of the earth and ocean, the bottom of the ocean, near the sea floor and at the top of the ocean, near the air-sky interface.
Each of the different regions will have different boundary conditions. We will consider boundary conditions of the Ekman layer in the upper ocean:[2]
where 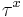 and
and 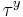 are the components of the surface stress,
are the components of the surface stress, 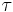 , of the wind field or ice layer at the top of the ocean and
, of the wind field or ice layer at the top of the ocean and 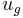 and
and 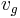 are the geostrophic flows in the
are the geostrophic flows in the 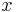 and
and 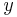 directions – as
directions – as 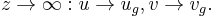
Solution
These differential equations can be solved to find:
This variation of horizontal velocity with depth (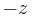 ) is referred to as the Ekman spiral, diagrammed above.
) is referred to as the Ekman spiral, diagrammed above.
By applying the continuity equation we can have the vertical velocity as following
Note that when vertically integrated the volume transport associated with the Ekman spiral is to the right of the wind direction in the Northern Hemisphere.
Experimental observations of the Ekman layer
There is much difficulty associated with observing the Ekman layer for two main reasons: the theory is too simplistic as it assumes a constant eddy viscosity, which Ekman himself anticipated,[3] saying
| “ | It is obvious that ![\ \left[\nu \right]](/2012-wikipedia_en_all_nopic_01_2012/I/c2d704f6a45289891dae0f02e9e38116.png) cannot generally be regarded as a constant when the density of water is not uniform within the region considered cannot generally be regarded as a constant when the density of water is not uniform within the region considered |
” |
and because it is difficult to design instruments with great enough sensitivity to observe the velocity profile in the ocean.
In the atmosphere
In the atmosphere, the Ekman solution generally overstates the magnitude of the horizontal wind field because it does not account for the velocity shear in the surface layer. Splitting the boundary layer into the surface layer and the Ekman layer generally yields more accurate results.[4]
In the ocean
The Ekman layer, with its distinguishing feature the Ekman spiral, is rarely observed in the ocean. The Ekman layer near the surface of the ocean extends only about 10 – 20 meters deep,[4] and instrumentation sensitive enough to observe a velocity profile in such a shallow depth has only been available since around 1980.[2] Also, wind waves modify the flow near the surface, and make observations close to the surface rather difficult.[5]
Instrumentation
Observations of the Ekman layer have only been possible since the development of robust surface moorings and sensitive current meters. Ekman himself developed a current meter to observe the spiral that bears his name, but was not successful.[6] The Vector Measuring Current Meter [7] and the Acoustic Doppler Current Profiler are both used to measure current.
Observations
The first observation of the Ekman spiral came in 1980 during the Mixed Layer Experiment.[8]
See also
References
- ^ [|Cushman-Roisin, Benoit] (1994). "Chapter 5 - The Ekman Layer". Introduction to Geophysical Fluid Dynamics (1st ed.). Prentice Hall. pp. 76–77. ISBN 0133533018.
- ^ a b [|Vallis, Geoffrey K.] (2006). "Chapter 2 – Effects of Rotation and Stratification". Atmospheric and Oceanic Fluid Dynamics (1st ed.). Cambridge, UK: Cambridge University Press. pp. 112–113. ISBN 0521849691.
- ^ Ekman, V.W. (1905). "On the influence of the earth's rotation on ocean currents". Ark. Mat. Astron. Fys. 2 (11): 1–52.
- ^ a b [|Holton, James R.] (2004). "Chapter 5 – The Planetary Boundary Layer". Dynamic Meteorology. International Geophysics Series. 88 (4th ed.). Burlington, MA: Elsevier Academic Press. pp. 129–130. ISBN 0123540151.
- ^ Santala, M. J.; Terray, E. A. (1992). "A technique for making unbiased estimates of current shear from a wave-follower". Deep-Sea Res. 39: 607–622. doi:10.1016/0198-0149(92)90091-7.
- ^ Rudnick, Daniel (2003). "Observations of Momentum Transfer in the Upper Ocean: Did Ekman Get It Right?". Near-Boundary Processes and their Parameterization (Manoa, Hawaii: School of Ocean and Earth Science and Technology).
- ^ Weller, R.A.; Davis, R.E. (1980). "A vector-measuring current meter". Deep-Sea Res. 27: 565–582. doi:10.1016/0198-0149(80)90041-2.
- ^ Davis, R.E.; de Szoeke, R.; Niiler., P. (1981). "Part II: Modelling the mixed layer response". Deep-Sea Res. 28: 1453–1475. doi:10.1016/0198-0149(81)90092-3.
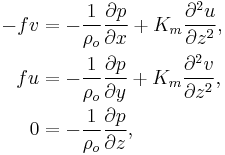
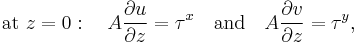
![\begin{align}
u &= u_g %2B \frac{\sqrt{2}}{fd}e^{z/d}\left [\tau^x cos(z/d - \pi/4) - \tau^y sin(z/d - \pi/4)\right ],
\\
v &= v_g %2B \frac{\sqrt{2}}{fd}e^{z/d}\left [\tau^x sin(z/d - \pi/4) %2B \tau^y cos(z/d - \pi/4)\right ].
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3631af1bb4f9cf6d19a815bfa622e8fa.png)
![\ w = \frac{1}{f\rho_o}\left [-\left (\frac{\partial \tau^x}{\partial x} %2B \frac{\partial \tau^y}{\partial y} \right )e^{z/d}sin(z/d) %2B \left (\frac{\partial \tau^y}{\partial x} - \frac{\partial \tau^x}{\partial y} \right )(1-e^{z/d}cos(z/d))\right ].](/2012-wikipedia_en_all_nopic_01_2012/I/85490deb84f78a1b847eb58ae46457e9.png)